この記事は何?
「ベイズ推論による機械学習入門」を読んでベイズ推論を理解した気がするので、本の3章で紹介されているアルゴリズムを実験してみました。
www.kspub.co.jp
ベルヌーイ分布の学習
本の3.2.1節で紹介されているベルヌーイ分布の学習と予測をUCI Machine Learning Repository: Breast Cancer Wisconsin (Diagnostic) Data Setに適用してみます。
このデータセットは乳がん診断の結果に関するデータセットであり、診断結果が良性か悪性かという情報が与えられています。
データセットのサイズはであり、良性のレコード数は357、悪性のレコード数は212でした。
確率変数を、診断結果が良性のときに
、悪性のときに
と定義します。
2値を取る離散の事象を表現するために、ベルヌーイ分布を考えます。
ベルヌーイ分布の共役事前分布であるベータ分布を考えます。
すると、事後分布は以下で与えられます、詳しくは本のP78を参照してください。
それではベルヌーイ分布の学習を実装してみます。といっても、を計算するだけですが……
def fit(X, a, b): # X: numpy array ([0, 1, 0, 1, ..., ]) # a, b: hyper parameter of the prior distribution N = X.shape[0] hat_a = np.sum(X) + a hat_b = N - np.sum(X) + b return hat_a, hat_b
ベルヌーイ分布の学習を上のデータセットに適用します。事前分布のパラメータはとしました。
学習の結果、が得られました(上式に代入するだけで求められます)。
実際に事前分布・事後分布を見てみましょう、下図の左側は事前分布、右側は事後分布を表しています。
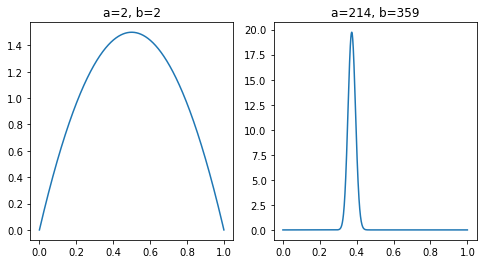
事後分布はあたりの部分でピークが見られます。
カテゴリ分布の学習
本の3.2.2節で紹介されているカテゴリ分布の学習と予測を
UCI Machine Learning Repository: Adult Data Setに適用してみます。
このデータセットは人口調査のデータセットであり、人種情報(White, Asian-Pac-Islander, Amer-Indian-Eskimo, Other, Black)が与えられています。
データセットのサイズはであり、各人種のレコード数は以下の通りです。
| 属性 | サイズ |
|---|---|
| White | 27816 |
| Black | 3124 |
| Asian-Pac-Islander | 1039 |
| Amer-Indian-Eskimo | 311 |
| Other | 271 |
確率変数を各属性に対応する1-hotベクトルと定義します。
例えば、"White"はと表し、"Black"は
と表します。
5値を取る離散の事象を表すために、カテゴリ分布を考えます。
カテゴリ分布の共役事前分布であるディリクレ分布を考えます。
すると、事後分布は以下で与えられます、詳しくは本のP82を参照してください。
それではカテゴリ分布の学習を実装してみます。事前分布のパラメータに各属性のレコード数を足すだけです。
def fit(S, alpha): # S: numpy array, shape: (N, K) # alpha: hyper parameter of the prior distribution hat_alpha = np.sum(S, axis=0) + alpha return hat_alpha
とすると、
が得られました。
は5次元(和が1になるという制約条件を考えれば4次元ですが)なので、事前分布・事後分布の描画はちょっと難しいです。。。
ポアソン分布の学習
本の3.2.3節で紹介されているポアソン分布の学習と予測を
UCI Machine Learning Repository: Wine Quality Data Set
に適用してみます。
このデータセットはワインの質に関するデータセットであり、ワインの質を0から10の離散値で表しています。
赤ワインと白ワインのデータセットがありますが、今回は白ワインのデータセットを使います。
データセットのサイズはであり、ワインの質に対応するレコード数は下表の通りです。
| ワインの質 | レコード数 |
|---|---|
| 3 | 20 |
| 4 | 163 |
| 5 | 1457 |
| 6 | 2198 |
| 7 | 880 |
| 8 | 175 |
| 9 | 5 |
確率変数をワインの質を表す離散値で定義します。
この事象を表現するために、ポアソン分布を考えます。
ポアソン分布の共役事前分布であるガンマ分布を考えます。
すると、事後分布は以下で与えられます、詳しくは本のP85を参照してください。
それではポアソン分布の学習を実装してみます。
def fit(X, a, b): # X: numpy array [6, 5, 9, ...] # a, b: hyper parameter of the prior distribution N = X.shape[0] hat_a = np.sum(X) + a hat_b = N + b return hat_a, hat_b
とすると、
が得られました。
実際に事前分布・事後分布を見てみましょう、下図の左側は事前分布、右側は事後分布を表しています。
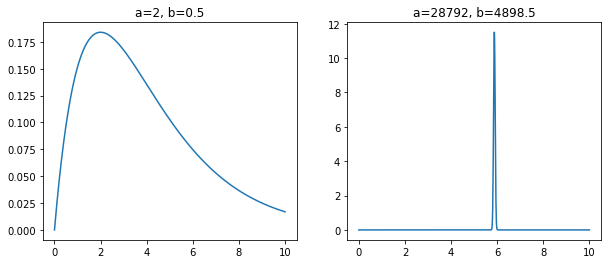
事後分布はあたりの部分でピークが見られます。
このことは、となることからも確かめられます。
せっかくなのでサンプリングもやってみます。
ここでは比較のため、訓練データのヒストグラム・MAP推定の結果得られたを用いた
からサンプリング・ベイズ推論による予測分布
からサンプリングの3つの結果を示します。
ここで、で与えられます、詳しくは本のP86を参照してください。
訓練データのヒストグラム・からサンプリング・
からサンプリングした結果を下図に示します。
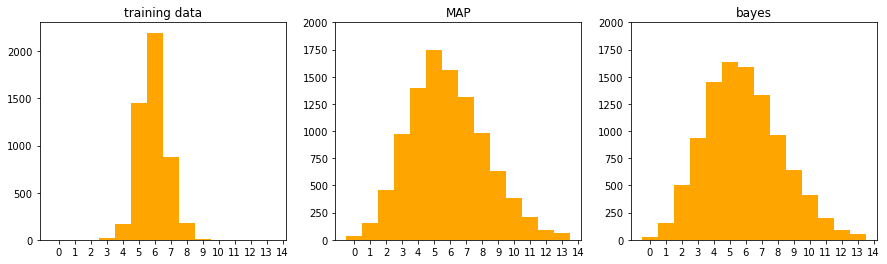
サンプリングの結果、0~2や9~13の値も結構出てきています、もう少し尖って欲しいが…?
1次元ガウス分布の学習と予測
本の3.2.3節で紹介されている平均・精度が未知の場合のガウス分布の学習と予測をUCI Machine Learning Repository: Wine Quality Data Setに適用してみます。
ポアソン分布の学習と予測で用いたデータセットですが、このデータセットにはワインの質以外にも、ワインのpHが与えられています。
pHについてのヒストグラムを下図に示します。
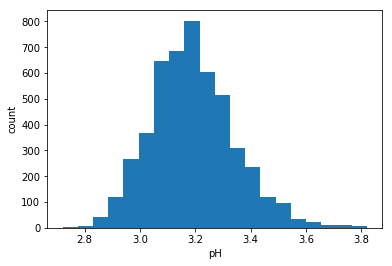
確率変数をワインのpHを表す実数値で定義します。
この事象を表現するために、ガウス分布を考えます。
ガウス分布の共役事前分布であるガウス・ガンマ分布を考えます。
するとに関する事後分布は以下で与えられます。
また、に関する事後分布は以下で与えられます。
これらの導出は本のP95を参照してください。
それではガウス分布の学習を実装してみます。
def fit(X, m, beta, a, b): # X: numpy array # m, beta, a, b: hyper parameter of the prior distribution N = X.shape[0] hat_beta = N + beta hat_m = 1 / hat_beta * (np.sum(X) + beta * m) hat_a = N / 2 + a hat_b = 1 / 2 * (np.sum(X ** 2) + beta * (m ** 2) - hat_beta * (hat_m ** 2)) + b return hat_beta, hat_m, hat_a, hat_b
とすると、
が得られました。
実際に事前分布・事後分布を見てみましょう、下図の左側は事前分布、右側は事後分布を表しています。
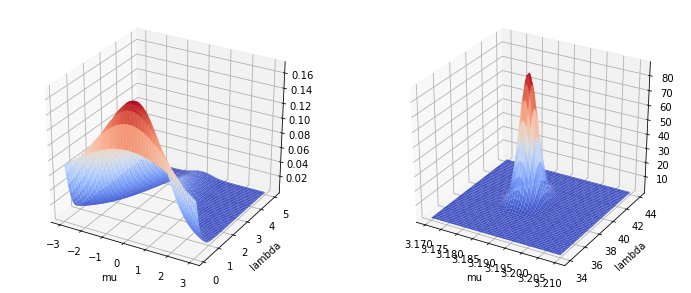
あたりの部分でピークが見られます。
事前分布はべちゃーってなっていますが、事後分布はピシッてなっているのが良いですね(は?)
その他
事後分布が解析的に求まるなら実装も簡単でした、次は4章の混合モデルと近似推論について実装していきます