この記事は何?
「情報検索 検索エンジンの実装と評価」Advent Calendarの2日目の記事です。
2章の「基本技術」をまとめます。
検索エンジンのコアとも言える転置インデックスについて紹介し、転置インデックス上でクエリ処理がどのように行われるのかを解説します。
また、再現率や適合率をはじめとする有効性指標や、応答時間やスループットなどの効率指標を紹介します。
転置インデックス
転置インデックスとは, 簡単にいえば, テキストコレクション
の中でタームがどこで出現しているかを指し示す地図のようなものである.
転置インデックスは、テキストコレクション中のタームからなる辞書および、タームが出現するドキュメント番号などを記録するポスティングリストからなります。
「ロミオとジュリエット」の第1幕第1場からのテキストの断片を用いて、転置インデックスを紹介します。
| ドキュメント番号 | 内容 |
|---|---|
| 1 | Do you quarrel, sir? |
| 2 | Quarrel sir! no, sir! |
| 3 | If you do, sir, I am for you: I serve as good a man as you. |
| 4 | No better. |
| 5 | Well, sir. |
転置インデックスは、記録するデータの種類によって4つのタイプに分類されます。
| スキーマ依存型 | ドキュメント番号インデックス | それぞれのタームについて、出現するドキュメント番号を記録する |
|---|---|---|
| 頻度インデックス | ドキュメント番号および頻度を記録する | |
| ポジションインデックス | ドキュメント番号、頻度、出現位置を記録する | |
| スキーマ非依存型 | スキーマ非依存型インデックス | バラバラのドキュメントを1つの大きなドキュメントとみなし、出現位置を記録する |
上の「ロミオとジュリエット」の例を、ポジションインデックス、スキーマ非依存型インデックスで表現してみます。
各インデックスの形式ですが、
- ポジションインデックス:
- スキーマ非依存型インデックス:
ただし、をリストの長さ、
をドキュメント番号、
をターム
が文書番号
に出現した頻度、
を出現位置として表します。
| ターム | ポジションインデックス | スキーマ非依存型インデックス |
|---|---|---|
| a | 1; (3, 1, <13>) | 1; 21 |
| am | 1; (3, 1, <6> ) | 1; 14 |
| as | 1; (3, 2, <11, 15>) | 2; 19, 23 |
| better | 1; (4, 1, <2>) | 1; 26 |
| do | 2; (1, 1, <1>), (3, 1, <3>) | 1; 26 |
| for | 1; (3, 1, <7>) | 1; 15 |
| good | 1; (3, 1, <12>) | 1; 20 |
| i | 1; (3, 2, <5, 9>) | 2; 13, 17 |
| if | 1; (3, 1, <1>) | 1; 9 |
| man | 1; (3, 1, <14>) | 1; 22 |
| no | 2; (2, 1, <3>), (4, 1, <1>) | 2; 7, 25 |
| quarrel | 2; (1, 1, <3>), (2, 1, <1>) | 2; 3, 5 |
| serve | 1; (3, 1, <10>) | 1; 18 |
| sir | 4; (1, 1, <4>), (2, 2, <2, 4>), (3, 1, <4>), (5, 1, <2>) | 5; 4, 6, 8, 12, 28 |
| well | 1; (5, 1, <1>) | 1; 27 |
| you | 2; (1, 1, <2>), (3, 3, <2, 8, 16>) | 4; 2, 10, 16, 24 |
例えばターム"as"について、ドキュメント番号3の11番目と15番目に現れるので、ポジションインデックスは"3; 2, <11, 15>"となります。
また、5つのドキュメントを1つの大きなドキュメントとみなすと、"as"は19番目と23番目に現れるので、スキーマ非依存インデックスは"2; 19, 23"となります。
例えば"do"が含まれるドキュメント番号について、ポジションインデックス:"do"に対応するポスティングリスト"2; (1, 1, <1>), (3, 1, <3>)"を辿ることで、ドキュメント番号1および3に含まれる…ということが分かります。
検索アルゴリズム
あるタームが含まれるドキュメントを見つけたい…という検索から一歩進んで、以下の複雑な検索アルゴリズムについて紹介します。
- フレーズ検索:"quarrel sir"が含まれるドキュメントを見つけたい
- ランキング検索:クエリへの予測関連度でドキュメントをランキングしたい
- 論理検索:AND・OR・NOTからなる論理演算子を利用して検索したい
準備
検索アルゴリズムを紹介する前に、転置インデックスにおける基本的な処理を紹介します。
:ターム
が位置
より後で最初に出現する位置を返す
:ターム
が位置
より前で最後に出現する位置を返す
例えば、ターム"witch"に対するポスティングリストに対して、
となります。
フレーズ検索
フレーズ検索は個のタームからなるフレーズが与えられたときに、すべての出現区間
を発見します。
例えば、以下の"first"と"witch"に対するポスティングリストについて、"first witch"でフレーズ検索した場合は、
では、本題のフレーズ検索のアルゴリズムを紹介します。
def nextPhrase(terms, position): """ positionの後方で最初にフレーズが出現する位置を特定する """ # フレーズにおけるターム数 n = len(terms) # タームが順番に並んでいる位置を求める v = position for i in range(n): v = next_(terms[i], v) # タームが順番に並んでいなければ終了 if v == np.inf: return (np.inf, np.inf) # タームが順番に並んでいる最小区間を求める u = v for i in range(n - 2, -1, -1): u = prev_(terms[i], u) # タームが全て隣り合って出現している if v - u == n - 1: return (u, v) # uから再検索 else: return nextPhrase(terms, u)
上のポスティングリストを例にして、アルゴリズムがどう動作するか確認します。
まず、タームが順番に並んでいる位置を求めます
次に、タームが順番に並んでいる最小区間を求めます
残念ながら、なので、フレーズ検索結果候補ではありません。
次は、から検索を行います。
次に、タームが順番に並んでいる最小区間を求めます
なので、フレーズ検索結果候補です!
を返します。
next, prevの実装について
本ではおよび
の実装について、以下の3つを取り上げていました。
- バイナリサーチ
- シーケンシャルスキャン
- ギャロップサーチ(本の推し実装)
例えばバイナリサーチで実装すると、以下のようになります。
def binarySearchNext(term, low, high, current): """ [low, high)の区間で, currentの後方で最初にtermが出現する位置を特定する - POSTING_LIST[low] <= current - POSTING_LIST[high] > current """ while high - low > 1: mid = (low + high) // 2 if INVERTED_INDEX[term][mid] <= current: low = mid else: high = mid return high def next_(term, current): if term not in INVERTED_INDEX or INVERTED_INDEX[term][-1] <= current: return np.inf if INVERTED_INDEX[term][0] > current: return INVERTED_INDEX[term][0] pos = binarySearch(term, 0, len(INVERTED_INDEX[term]), current) return INVERTED_INDEX[term][pos]
def binarySearchPrev(term, low, high, current): """ [low, high)の区間で, currentの前方で最後にtermが出現する位置を特定する - POSTING_LIST[low] < current - POSTING_LIST[high] >= current """ while high - low > 1: mid = (low + high) // 2 if INVERTED_INDEX[term][mid] < current: low = mid else: high = mid return low def prev_(term, current): if term not in INVERTED_INDEX or INVERTED_INDEX[term][0] >= current: return -np.inf if INVERTED_INDEX[term][-1] < current: return INVERTED_INDEX[term][-1] pos = binarySearchPrev(term, 0, len(INVERTED_INDEX[term]), current) return INVERTED_INDEX[term][pos]
ランキング検索
クエリへの予測関連度でドキュメントをランキングすることを考えます。
予測関連度を求めるために以下の基本的な特徴量を利用します。
- ドキュメントにクエリタームが出現する回数(ターム頻度)
- ドキュメントにクエリタームが近く出現しているか(ターム近接度)
- タームが出現するドキュメントの数(ドキュメント頻度)
- ドキュメントの長さ
本ではランキング検索として、ベクトル空間モデルおよび近接度ランキングが紹介されていました。
ベクトル空間モデルはターム頻度およびドキュメント頻度を扱う手法で、近接度ランキングはターム近接度を扱う手法です。
(ベクトル空間モデルにおいて、ドキュメントの長さは正規化のために利用されています。)
ベクトル空間モデル
ベクトル空間モデルは1960年代から1990年代にかけて開発された古典的なランキング検索手法です。
ベクトル検索モデルでは、クエリとドキュメントをそれぞれベクトル化し、クエリベクトルと各ドキュメントベクトルのなす角を計算してスコアリングします。
下の図では、検索クエリをベクトルと表し、2つのドキュメントをベクトル
で表しています。
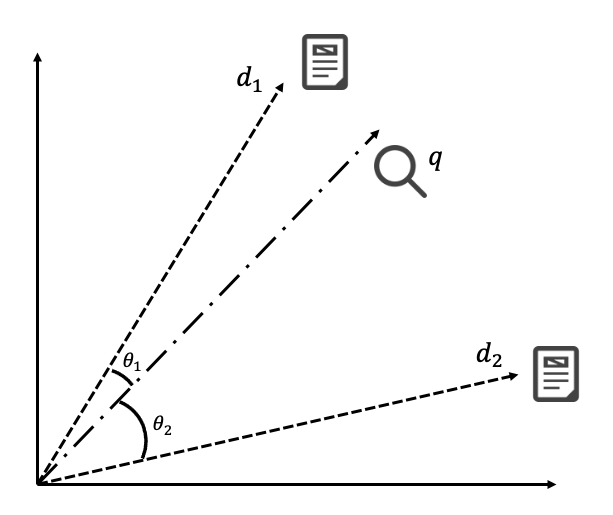
と
のなす角
は
と
のなす角
よりも小さいので、ドキュメント1をドキュメント2よりも上位にランキングします。
2つのベクトルのなす角自体でスコアリングするのは、以下の式で与えられるコサイン近似度でスコアリングするのと等価です。
次に、クエリやドキュメントをどうベクトル化するかについて考えます。
ベクトル化については様々な方法が考えられてきましたが、基本的かつ重要な方法としてTF-IDFによる重み付けが紹介されています(散々語り尽くされた話題だとは思いますが…)。
TF-IDFによる重み付けでは、「ターム頻度の関数」と「ドキュメント頻度の逆数
の関数」を掛け合わせます。
ターム頻度の関数としては、例えば以下の関数が使われます。
ドキュメント頻度の逆数の関数としては、例えば以下の関数が使われます。
TF-IDFの例として、あらためて以下のドキュメントセットを利用して説明します。
| ドキュメント番号 | 内容 |
|---|---|
| 1 | Do you quarrel, sir? |
| 2 | Quarrel sir! no, sir! |
| 3 | If you do, sir, I am for you: I serve as good a man as you. |
| 4 | No better. |
| 5 | Well, sir. |
ターム"sir"について、ドキュメント2には2回出現しており、5つのドキュメント中4つのドキュメントで"sir"が出現しています。
ゆえに、TF-IDFは以下のように計算されます。
他のタームについても同様にTF-IDFを計算することで、ドキュメントベクトルおよびクエリベクトルが得られます。
近接度ランキング
あるドキュメントの中でクエリのタームが互いに近くに出現しているのであれば、そのドキュメントはクエリに関連しているであろうと考えられます。
ここで、フレーズ検索ではタームの出現順序まで気にしていましたが、近接度ランキングでは出現順序は気にしないことに注意してください。
タームベクトルが与えられたとき、このベクトルの成分をすべて含むコレクション中の区間
をカバーと定義します。
このとき、 には、ベクトルの成分をすべて含むより狭い区間
を含まないこととします。
カバーの例として、あらためて以下のドキュメントセットを利用して説明します。
| ドキュメント番号 | 内容 |
|---|---|
| 1 | Do you quarrel, sir? |
| 2 | Quarrel sir! no, sir! |
| 3 | If you do, sir, I am for you: I serve as good a man as you. |
| 4 | No better. |
| 5 | Well, sir. |
タームベクトル<"you", "sir">について、区間[1:2, 1:4], [3:2, 3:4], [3:4, 3:8]はカバーとなっています。(ドキュメント番号:ターム位置)
区間[3:4, 3:16]はカバー[3:4, 3:8]を含んでいるため、カバーではありません。
カバーの範囲が狭いと関連度が高い、多くのカバーを持つドキュメントの方が関連度が高いという仮定から、近接度ランキングスコアを以下のように定義します。
あるドキュメントがカバー
を含むとき、そのスコアを
と定義します。
次に、カバーを発見するアルゴリズムを紹介します。
以下のnextCover(terms, position)は、position以降のカバーを返す関数です。
def nextCover(terms, position): # マッチ位置の最後尾を求める v = max([next_(term, position) for term in terms]) # マッチしなかったら終了 if v == np.inf: return (np.inf, np.inf) # カバーを得るために最も狭い区間(左端)を求める u = min([prev_(term, v + 1) for term in terms]) return (u, v)
以下のポスティングリストを例に、タームベクトル<"first", "witch">に対して上のアルゴリズムがどのように動くかを説明します。

について、まずマッチ位置の最後尾を求めます。
より、となります。
次に、カバーの左端を求めます。
より、となります。
よって、となります。
論理検索
論理検索では論理演算子"AND", "OR", "NOT"をサポートした検索手法です。
ランキング検索とは違い、検索結果はスコア付けはされず、単にマッチしたドキュメント集合が返却されます。
スキーマ依存型転置インデックスを前提として、論理検索のアルゴリズムを紹介します。
ただし、論理検索のアルゴリズムは上で紹介した近接ランキングにおけるカバー発見アルゴリズムとほぼ同じです。
準備として、論理検索クエリに対する以下の関数を定義します。
:ドキュメント
の後方において、
に対する最初の候補解の終了場所
:ドキュメント
の前方において、
に対する最後の候補解の開始場所
タームに対しては以下のように定義します。
:
から後方において、ターム
を含む最初のドキュメント番号
:
から前方において、ターム
を含む最後のドキュメント番号
"AND"と"OR"に対しては以下のように定義します。
"NOT"に関してはド・モルガン法則を適用することで"NOT term"の表現によるクエリに変換することができるため、を定義する必要はありません。
論理検索クエリの処理を、あらためて以下の表の例を利用して説明します
| ドキュメント番号 | 内容 |
|---|---|
| 1 | Do you quarrel, sir? |
| 2 | Quarrel sir! no, sir! |
| 3 | If you do, sir, I am for you: I serve as good a man as you. |
| 4 | No better. |
| 5 | Well, sir. |
(("quarrel" OR "sir") AND "you")というクエリについて、
を実行してみます。
以上を利用して、論理検索クエリは以下のアルゴリズムで処理できます。
def nextSolution(Q, position): # 区間[u, v]を求める v = docRight(Q, position) if v == np.inf: return np.inf u = docLeft(Q, v + 1) # 区間長さ=1 if u == v: return u else: return nextSolution(Q, v)
…カバー発見アルゴリズムとほぼ同じです。
評価
1章でも紹介しましたが、検索エンジンは有効性と効率の2つの側面から評価されます。
ここでは基本的な評価手法のみ紹介されていましたが、12章・13章でより詳細に有効性・効率について解説されます。
有効性の評価
再現率や適合率やF値の話です。
↓が非常に分かりやすくまとまっています。
特に情報検索で注意すべき点として、precision@kやrecall@kのkをいくつにすべきかという話があります。
小さなkの値は, ユーザにとっては素早く検索結果を得ることが重要であり, 数個の検索結果を得たい場合に相当する.
大きなkの値は, ユーザができる限り多くの情報を得ようとしており, 結果リストの詳細まで検討したいと考えている場合に相当する.
例として、Web検索ではランキング上位が重要なのに対し、法律関係の検索では徹底的な検索が重要であると紹介されています。
テストコレクションの構築
1章でテストコレクションについて紹介しました。
有効性を評価するためには、各トピックに対するドキュメントごとの関連性判定が必要になります。
ただし、ドキュメント集合は通常とても大きいため、ドキュメント全てに対して関連性判定するのは非現実的です。
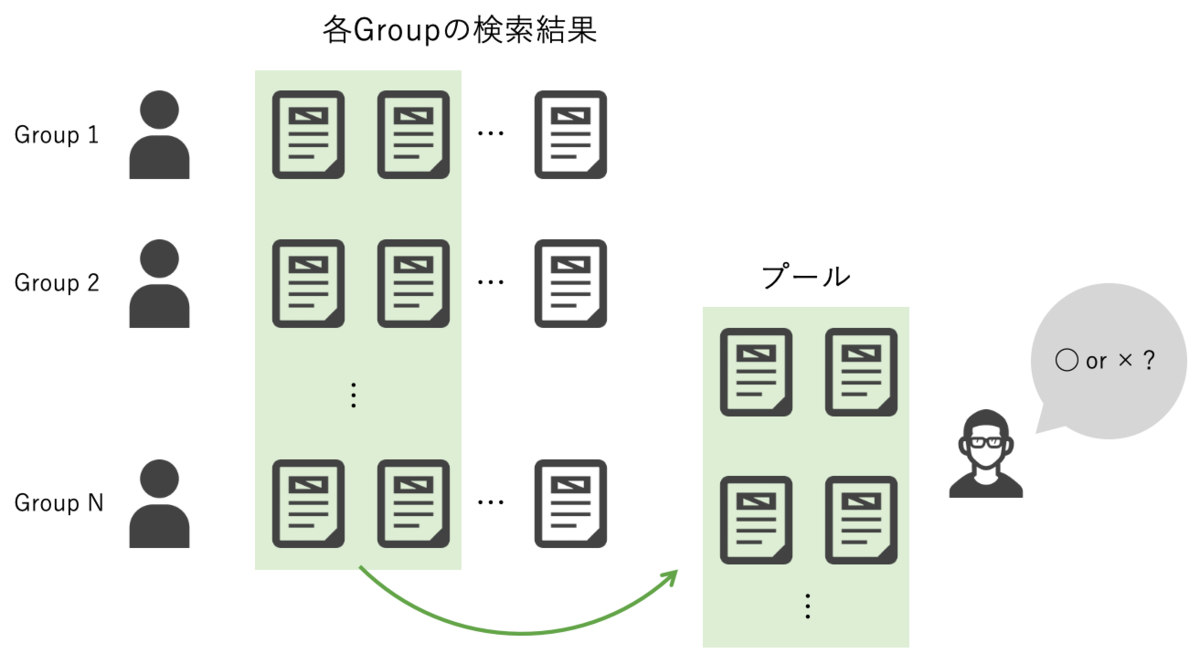
TRECではプーリングという手法で関連性判定の工数を削減しています。
プーリングは、TREC実験の参加者から検索結果を集め、各検索結果の上位をまとめた集合に対して、関連性判定をする手法です。
プーリングによって、関連性判定対象のドキュメント数を大幅に削減できます。
一方で、プールに現れず関連性評価されていないドキュメントを真に新しい検索手法が発見した場合、そのドキュメントは非関連として評価されてしまう問題があります。
12章ではプーリングの問題をさらに深掘りして解説しています。
効率の評価
効率についても1章で紹介しましたが、効率測定について注意すべき点が紹介されていました。
- 測定前に検索システムをリスタートもしくはリセットし、メモリに残された検索用データをリセットする
- OSのI/Oキャッシュもリセットする
- システムのリセットを挟んで複数回効率測定を行い、平均値を報告する
(測定結果結構ブレるので、平均値だけじゃなく中央値も見ておいた方が良いという知見があります…)
まとめ
フレーズ検索や論理検索のアルゴリズムはいくつかの書籍で紹介されていますが、Buttcher本は多少複雑な方法を紹介している気がします…
(この本、結構上級者向けなのでは?)