この記事は何?
生態学データ解析 - 本/データ解析のための統計モデリング入門の第9章ではGLMを題材としたMCMCが紹介されています. この本ではMCMCのソフトウェアとしてWinBUGSが使われていますが,インストールバトルに負けたのでPyStanを使って第9章の例題を動かしてみます.
例題で扱うデータ
目的変数を,説明変数を
とします.
は平均
のポアソン分布に従うと仮定し,
とします.
今回使うデータはhttp://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/gibbs/d.RDataからダウンロードしました,Rのオブジェクトなのでcsvに変換してください.
データの確認
%matplotlib inline import pystan import numpy as np import pandas as pd import matplotlib.pyplot as plt beta1 = 1.5 beta2 = 0.1 data_file = "data.csv" df = pd.read_csv(data_file) X = df["x"] y = df["y"] plt.plot(X, y, "bo") xx = np.linspace(3, 7) yy = np.exp(beta1 + beta2 * xx) plt.plot(xx, yy, "--") plt.xlim(2.9, 7.1) plt.ylim(2, 13)
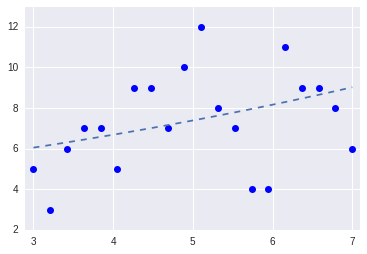
各点はを,波線はデータ生成に用いられたポアソン分布の平均
を表します.
PyStanでMCMC
まずstanのファイルを用意します.
data {
int<lower=1> N;
real X[N];
int<lower=0> y[N];
}
parameters {
real beta1;
real beta2;
}
model {
beta1 ~ normal(0, 1.0E4);
beta2 ~ normal(0, 1.0E4);
for (i in 1:N) {
y[i] ~ poisson_log(beta1 + beta2 * X[i]);
}
}
parametersブロックで指定したがサンプリングされます.
次にPyStan側のコードです.
N = X.shape[0] stan_data = {"N": N, "X": X, "y": y} fit = pystan.stan(file="glm_mcmc.stan", data=stan_data, iter=1600, chains=3, thin=3, warmup=100)
これでサンプリングが行われます.実行結果を確認します.
print(fit)
Inference for Stan model: anon_model_798d2fcd5dc937ab5386282eba6b60b2.
3 chains, each with iter=1600; warmup=100; thin=3;
post-warmup draws per chain=500, total post-warmup draws=1500.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
beta1 1.56 0.02 0.37 0.8 1.31 1.55 1.81 2.26 281 1.0
beta2 0.08 4.2e-3 0.07 -0.05 0.04 0.08 0.13 0.22 285 1.0
lp__ 143.98 0.05 0.98 141.55 143.54 144.3 144.68 144.95 353 1.0
Samples were drawn using NUTS(diag_e) at Sun Jun 26 00:22:24 2016.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
実行結果中のRhatの値から収束していると見なすことができます.
の平均が1.56,
の平均が0.08と推定されています.真の値はそれぞれ1.5,0.1でした.
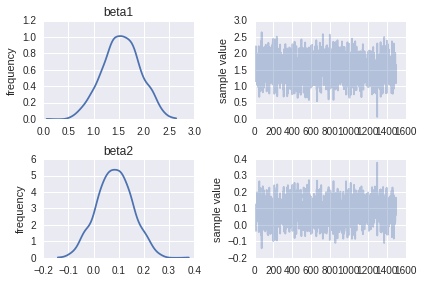
事後確率の分布も見てみます.
fit.plot() plt.tight_layout()