この記事は何?
2つの母平均の差の検定を行うとき、まずは対応のないt検定(unpaired t-test)を考えると思います。
対応のないt検定には以下の仮定が存在します。
- 母集団が互いに独立に正規分布に従う(独立性の仮定・正規性の仮定)
- 母分散が等しい(等分散性の仮定)
独立性の仮定が成り立たない場合はお手上げですが、実務では独立性の仮定が成り立たないケースはそこまで発生しないのではないでしょうか。
等分散性の仮定が成り立たない場合はWelchのt検定(Welch's t-test)を使います。
この記事では、正規性の仮定が成り立たない場合について考えてみます。
いくつかの記事によると、「unpaired t-testは正規性の仮定については鈍感である」と主張されています。
実際には
が正規分布でなくても,
が大きければ中心極限定理により
は正規分布に近づくので,この検定は母集団が正規分布かどうかには鈍感です。データの分布が正規分布かどうかの検定をしてから t検定を行う必要はまったくありません。
まず,母集団の正規性,あるいはデータの正規性については,t検定は頑健だといわれています。それは,サンプルサイズが十分大きければ,母集団が正規分布でなくとも,推定する差の分布は正規分布に近づくからです(中心極限定理)。
In fact, as the sample size in the two groups gets large, the t-test is valid (i.e. the type 1 error rate is controlled at 5%) even when X doesn't follow a normal distribution.
これらの主張がどの程度妥当なのか、false positive rateを求めて確認してみます。
false positive rateの確認
unpaired t-testにおける2つの母集団をそれぞれとします。
母平均が共に等しいケースでは、有意水準とすると、「本当は母平均に差はないのに、有意に差がある(false positive)」と言ってしまう割合が5%になるはずです。
まずは、正規性の仮定が成り立っているケースで、false positive rateを確かめてみます。
母集団が互いに独立にに従うとし、標本をそれぞれ
とします。今回はとしました。
有意水準として、得られた標本を用いてunpaired t-testを実施し、有意に差があるかどうかを検定します。
この手続きを回行い、
回の検定の中で何回有意差があったのか(false positive rate)を求めてみます。
以下Pythonコードです(scipyのstats.ttest_indを用いています)
実行してみたところ、回の検定の中で543回有意差がありました。
false positive rate=0.0543となり、おおよそ有意水準と一致しています!
参考に、p値の累積分布を描きました。
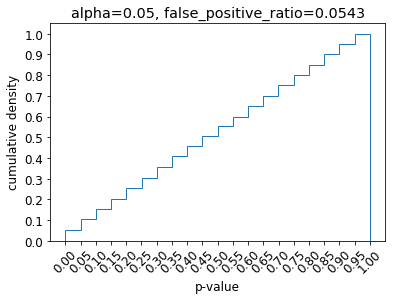
次に、正規性の仮定が成り立っていないケースで確かめてみます。
今度は、母集団が互いに独立にポアソン分布に従うとします。
が大きいと正規分布で近似できてしまって面白くないので、2という小さめの値にしました。
の形を描いておきます。
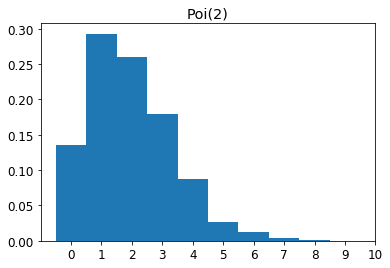
上と同じように、とし、
回検定を行ったところ、519回有意差がありました。
false positive rate=0.0519となり、おおよそ有意水準と一致しています!
先ほどはと、サンプルサイズが大きめなケースを考えました。
今度は、サンプルサイズを小さくとして、同様の実験を行ってみます。
結果は、false positive rate=0.0497となりました、意外と合ってますね。。。
もうすこしひどい分布として、ガンマ分布を考えます。
母集団が互いに独立にガンマ分布に従うとします。ヒストグラムを描いておきます。
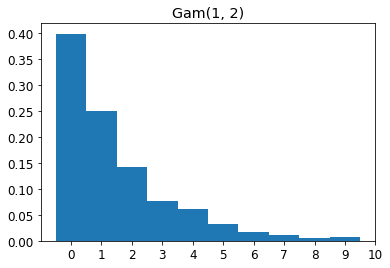
としたときはfalse positive rate=0.0504,
としたときはfalse positive rate=0.0419という結果が得られました。
サンプルサイズが小さいとき、false positive rateは有意水準よりも比較的小さくなることが分かりました。
false positive rateが小さくなる分には困らない(より厳しい検定をしている)と思います。
まとめ
以上の実験結果をまとめます。
| 母集団の分布 | サンプルサイズ | false positive rate |
|---|---|---|
| 100 | 5.43% | |
| 100 | 5.19% | |
| 10 | 4.97% | |
| 100 | 5.04% | |
| 10 | 4.19% |
上の実験の範囲ですが、「unpaired t-testは正規性の仮定は成り立たなくても、false positive rateについては心配しなくても大丈夫」ということが言えました。
サンプルサイズが10程度でも問題にならなかったのは結構ビックリです。
もちろん、「多峰性だったらどうなの?」や「非対称性がひどかったらどうなるの?」など、調べていない部分もありますが。。。
今回はfalse negative rate(本当は差があるのに、差が無いと言ってしまう)については考えていません。
有意水準・検出力・効果量から検定に必要なサンプルサイズを求めて、そのサンプルサイズにおける検定を繰り返すことでfalse negative rateを出すことはできると思います。
とはいえ、とてつもなく大きい効果量でない限り、検定にはそこそこのサンプルサイズが必要になってしまうため、小さいサンプルサイズの実験がやりづらいです。。。
効果量大きくすると分散も変わってきて、サンプルサイズ計算をやりにくいという話もあり。。。